Introduction
There are two things I want to look at in this post. Firstly, what performance improvement is available if you try and improve the way you move data around using the cMesh and secondly, how would you measure that improvement.
The reason I'm spending time looking at this is that inter-core communication is the Achilles Heal of distributed memory multi-processors. There are a few algorithms that do not require the cores to share data (known as "embarrassingly parallel") but most do. Given that the whole purpose of using a parallel processing environment is performance, using the best communication strategy is crucial.
To be able to decide which is best, you need to be able to measure it. I used the e_ctimer functions to measure wall-clock performance of four different strategies. To gain some additional insight into what is going on, I used the slightly more complicated eMesh configuration registers to measure the wait times due to mesh traffic.
My conclusion is that, while some small improvements are available by using a carefully thought out strategy, the most important factor is now efficient your algorithm is.
Getting Started
I'm using the COPRTHR-2 beta pre-processor that is available here. At the time of writing it only runs on the Jan 2015 Parallella image.
$ uname -a
Linux parallella 3.14.12-parallella-xilinx-g40a90c3 #1 SMP PREEMPT Fri Jan 23 22:01:51 CET 2015 armv7l armv7l armv7l GNU/Linux
However, while I'm using COPRTHR-2 everything I use is available in COPRTHR-1 and the MPI add-in.
To have a look at the code, use git:
$git clone -b broadcastStrat https://github.com/nickoppen/passing.git
In my previous post on passing strategies I looked at two broadcast strategies that were essentially the same other than that one had a barrier function on every iteration. It turns out that the barrier function completely dominates the time required by the function. On examination a barrier per iteration was not needed so the non-barrier version was the clear winner. This strategy is my base case.
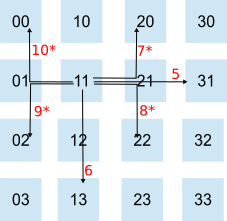
The base strategy passed all values "up". That is, each core passes the data to the core with a global id one greater than itself looping back to zero when it reached the "last" core with global id equal to fifteen. It stopped when it got back to it's own global id.
Thus, the core with global id 5 would send it's data to the other cores in the following order:
6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 0, 1, 2, 3, 4 and stop because 5 is next.
I need to do this sort of distribution in my neural network program and when I came to write that routine I thought that the original strategy was a bit complicated. Why not just send the data to the core with global id 0 then 1 then 2 and so on until 15, skipping the local node.
Thus core 5 would send in the following order:
0, 1, 2, 3, 4, skip, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
I didn't think that this would be a more efficient way to send data but at least the code was simpler.
With both of the preceding strategies, the cores treat the epiphany as if is a linear array of cores. I thought that there might be some improvement by making more use of the vertical, north and south connections between the cores. To this end I came up with two strategies that ignored the artificially linear nature of the global id distribution.
There is a handy site that generates random number sequences. I generated sixteen of them and ordered my cores accordingly. I remove the local core address for each core and from there it was simply a matter of iterating through the array of cores. No further thought required.
In the final strategy, I tried to come up with a sending order that would try and reduce the number of cores trying to send data along the same channel at the same time. Thus reducing the number of clashes and therefore the amount of time the cores had to wait.
I used a "nearest first" strategy. Thus direct neighbours get the data first. For core 5:
Then I send to cores that are two hops away:
* Note: I have not changed the default "horizontal then vertical" communication strategy employed by the epiphany hardware.
Then, after two hops I do three hops, fours hops etc until all fifteen other cores have received the data. I also vary the initial direction, left first on the top row, then up on the second etc.
Both the "Random" and "Mapped" strategies require a different list of core base addresses for every core. In my kernel all cores get all lists but only use one. If space is tight, these lists could be stored in shared memory and each core would only copy down the list it is going to use.
As with my last post on data passing, I use the following to make the copy:
#define NEIGHBOUR_LOC(CORE, STRUCTURE, INDEX, SIZEOFTYPE) (CORE + ((unsigned int)STRUCTURE) + (INDEX * SIZEOFTYPE))
The #define slightly improves the readability in the inner loop:
The kernel is called 32 times with the amount of data being copied increasing from 1 to 32 integers (ints). The whole loop is repeated 10,000 times to add to the workload and get some more representative numbers.
The epiphany chip has two timers and they are implemented in hardware (so the best information comes from the Architecture Reference Document not the SDK Reference Document). They count downwards from their initial value.
The basic usage of a timer is as follows:
e_ctimer_set(E_CTIMER_0, E_CTIMER_MAX); // set timer register to its max value
start_ticks = e_ctimer_start(E_CTIMER_0, E_CTIMER_CLK); // start the timer to count clock ticks remembering the initial value
Note: I've used a C style #define to define an inline function with multiple lines. I've done this to avoid the overhead associated with a function call.
The mesh timer is a little more complicated. The start and stop are the same as above but you have to tell the epiphany what mesh event you want to time. You can time wait or access events to the CPU and/or to the four connections (see the MESHCONFIG register definitions in the Architecture Reference). To do this you need to set a value in the E_MESH_CONFIG register. Then, to be neat, you need to restore E_MESH_CONFIG back to what it was before you started.
To initialise the timer to measure all mesh wait ticks:
#define E_MESHEVENT_ANYWAIT1 0x00000200 // Count all wait events
int mesh_reg = e_reg_read(E_REG_MESHCFG); // make a copy of the previous value
int mesh_reg_timer = mesh_reg & 0xfffff0ff; // blank out bits 8 to 11
mesh_reg_timer = mesh_reg_timer | E_MESHEVENT_ANYWAIT1; // write desired event code in bits 8 to 11
e_reg_write(E_REG_MESHCFG, mesh_reg_timer); // write the new value back to the register
/* Note: the Architecture Reference document (Rev 14.03.11 pp. 148 - 149) seems to imply that bits 4 - 7 control E_CTIMER1 and bits 8 - 11 control E_CTIMER0. This is around the wrong way. Bits 4 - 7 control E_CTIMER0 and bits 8 - 11 control E_CTIMER1. */
Then you start your time as described above but using E_CTIMER_MESH_1 (for E_CTIMER1) and the timer will count the event type you requested.
Stopping is the same as above but then, to be neat you should put the register back to where it was prior to the initialisation:
e_reg_write(E_REG_MESHCFG, mesh_reg); // where mesh_reg is previous value
Again, I've defined inline functions for brevity and performance:
#define PREPAREMESHTIMER1(mesh_reg, event_type)...
#define STARTMESHTIMER1(start_ticks)...
#define STOPMESHTIMER1(stop_ticks)...
#define RESETMESHTIMER1(mesh_reg)...
To make it obvious that I'm using E_CTIMER_0 for the clock and E_CTIMER_1 for the mesh timer I've added a "0" and a "1" onto the end of my inline function calls.
I plotted the wall clock time of each passing algorithm:
First, let me say that I have NO IDEA why the graph shows time reductions at 9, 17 and 25 integers. Maybe someone who understands the hardware better than me could explain that.
Second, for small amount of data there are some significant gains to be had. The "mapped" strategy outperforms the base line strategy by between 10% to 25% if you are sending 11 integers or less.
Thirdly, as the inner loop comes to dominate the execution time, the difference between the algorithms decreases. Therefore, for larger amounts of data, being really clever in your program delivers increasingly diminishing returns. The 25% difference writing one int shrunk down to about 1% for 32 ints.
Finally, and this is not obvious from the wall clock chart, the improvements in performance come from a more efficient algorithm rather than from better use of the cMesh. As I improved the algorithms I could see the execution time reducing. This is more obvious in the following, somewhat surprising chart:
This chart shows the average number of clock ticks that the cores have to wait for all mesh events. If the reduction in execution time was due to a more efficient use of the cMesh then you would expect that the best performers ("Mapped" and "Random") would be waiting less than the other two strategies.
It seems that the outer loop with fewer iterations is faster at pumping out data into the mesh which is therefore more clogged. However, the increase in waiting time of the "Mapped" strategy was only 6% of the total execution time compared to 4.2% for "Pass Up" and "0 to 15". Thus the difference made a small contribution to the convergence of the strategies as the volume of data increased.
I must also add that the steady upwards trend shown in the above graph is somewhat over simplified. Initially I used 1,000 iterations. That showed the same trend but the lines jumped around all over the place. If you are measuring something that is only a small chuck of the total execution time (in this case, 4% - 6%) and something that is influenced by other factors (i.e. other core's mesh traffic) you need to repeat the test many many times.
Using the e_ctimer functions is a great way to test out alternative implementations. It is like using a volt meter when developing circuits. However, you may need to run your test many thousands of times to get repeatable, representative results.
The cMesh does a pretty consistent job of delivering the data. If one of the broadcast strategies was inherently better I would expect the performance difference to be maintained and even increase as the amount of data rises. If you use direct memory writes for large amounts of data, simple is probably best.
For low volumes, while some improvement is available by tweaking the delivery process, it is your program that determines the overall performance.
To have a look at the code, use git:
$git clone -b broadcastStrat https://github.com/nickoppen/passing.git
The Strategies
In my previous post on passing strategies I looked at two broadcast strategies that were essentially the same other than that one had a barrier function on every iteration. It turns out that the barrier function completely dominates the time required by the function. On examination a barrier per iteration was not needed so the non-barrier version was the clear winner. This strategy is my base case.
Base Strategy - "Pass Up"
The base strategy passed all values "up". That is, each core passes the data to the core with a global id one greater than itself looping back to zero when it reached the "last" core with global id equal to fifteen. It stopped when it got back to it's own global id.
Thus, the core with global id 5 would send it's data to the other cores in the following order:
6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 0, 1, 2, 3, 4 and stop because 5 is next.
Refinement 1 - "0 to 15"
I need to do this sort of distribution in my neural network program and when I came to write that routine I thought that the original strategy was a bit complicated. Why not just send the data to the core with global id 0 then 1 then 2 and so on until 15, skipping the local node.
Thus core 5 would send in the following order:
0, 1, 2, 3, 4, skip, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
I didn't think that this would be a more efficient way to send data but at least the code was simpler.
With both of the preceding strategies, the cores treat the epiphany as if is a linear array of cores. I thought that there might be some improvement by making more use of the vertical, north and south connections between the cores. To this end I came up with two strategies that ignored the artificially linear nature of the global id distribution.
Refinement 2 - "Random"
There is a handy site that generates random number sequences. I generated sixteen of them and ordered my cores accordingly. I remove the local core address for each core and from there it was simply a matter of iterating through the array of cores. No further thought required.
Refinement 3 - "Mapped"
In the final strategy, I tried to come up with a sending order that would try and reduce the number of cores trying to send data along the same channel at the same time. Thus reducing the number of clashes and therefore the amount of time the cores had to wait.
I used a "nearest first" strategy. Thus direct neighbours get the data first. For core 5:
Then, after two hops I do three hops, fours hops etc until all fifteen other cores have received the data. I also vary the initial direction, left first on the top row, then up on the second etc.
Both the "Random" and "Mapped" strategies require a different list of core base addresses for every core. In my kernel all cores get all lists but only use one. If space is tight, these lists could be stored in shared memory and each core would only copy down the list it is going to use.
The Implementation
Copying
As with my last post on data passing, I use the following to make the copy:
#define NEIGHBOUR_LOC(CORE, STRUCTURE, INDEX, SIZEOFTYPE) (CORE + ((unsigned int)STRUCTURE) + (INDEX * SIZEOFTYPE))
The #define slightly improves the readability in the inner loop:
for (i=firstI; i < lastI; i++)
*(int *)NEIGHBOUR_LOC(core[coreI], vLocal, i, (sizeof(int))) = vLocal[i];
Clock Timer
The epiphany chip has two timers and they are implemented in hardware (so the best information comes from the Architecture Reference Document not the SDK Reference Document). They count downwards from their initial value.
The basic usage of a timer is as follows:
e_ctimer_set(E_CTIMER_0, E_CTIMER_MAX); // set timer register to its max value
start_ticks = e_ctimer_start(E_CTIMER_0, E_CTIMER_CLK); // start the timer to count clock ticks remembering the initial value
// implement the code you want timed
stop_ticks = e_ctimer_get(E_CTIMER_0); // remember the final value
e_ctimer_stop(E_CTIMER_0); // stop timing
time = start_ticks - stop_ticks; // calculate the elapsed time in ticks
to stop the timer. Again I've #defined these lines:
#define STARTCLOCK0(start_ticks) e_ctimer_set(E_CTIMER_0, E_CTIMER_MAX); start_ticks = e_ctimer_start(E_CTIMER_0, E_CTIMER_CLK);
#define STOPCLOCK0(stop_ticks) stop_ticks = e_ctimer_get(E_CTIMER_0); e_ctimer_stop(E_CTIMER_0);
Note: I've used a C style #define to define an inline function with multiple lines. I've done this to avoid the overhead associated with a function call.
Mesh Timer
The mesh timer is a little more complicated. The start and stop are the same as above but you have to tell the epiphany what mesh event you want to time. You can time wait or access events to the CPU and/or to the four connections (see the MESHCONFIG register definitions in the Architecture Reference). To do this you need to set a value in the E_MESH_CONFIG register. Then, to be neat, you need to restore E_MESH_CONFIG back to what it was before you started.
To initialise the timer to measure all mesh wait ticks:
#define E_MESHEVENT_ANYWAIT1 0x00000200 // Count all wait events
int mesh_reg = e_reg_read(E_REG_MESHCFG); // make a copy of the previous value
int mesh_reg_timer = mesh_reg & 0xfffff0ff; // blank out bits 8 to 11
mesh_reg_timer = mesh_reg_timer | E_MESHEVENT_ANYWAIT1; // write desired event code in bits 8 to 11
e_reg_write(E_REG_MESHCFG, mesh_reg_timer); // write the new value back to the register
/* Note: the Architecture Reference document (Rev 14.03.11 pp. 148 - 149) seems to imply that bits 4 - 7 control E_CTIMER1 and bits 8 - 11 control E_CTIMER0. This is around the wrong way. Bits 4 - 7 control E_CTIMER0 and bits 8 - 11 control E_CTIMER1. */
Then you start your time as described above but using E_CTIMER_MESH_1 (for E_CTIMER1) and the timer will count the event type you requested.
Stopping is the same as above but then, to be neat you should put the register back to where it was prior to the initialisation:
e_reg_write(E_REG_MESHCFG, mesh_reg); // where mesh_reg is previous value
Again, I've defined inline functions for brevity and performance:
#define PREPAREMESHTIMER1(mesh_reg, event_type)...
#define STARTMESHTIMER1(start_ticks)...
#define STOPMESHTIMER1(stop_ticks)...
#define RESETMESHTIMER1(mesh_reg)...
To make it obvious that I'm using E_CTIMER_0 for the clock and E_CTIMER_1 for the mesh timer I've added a "0" and a "1" onto the end of my inline function calls.
The Results
I plotted the wall clock time of each passing algorithm:
First, let me say that I have NO IDEA why the graph shows time reductions at 9, 17 and 25 integers. Maybe someone who understands the hardware better than me could explain that.
Second, for small amount of data there are some significant gains to be had. The "mapped" strategy outperforms the base line strategy by between 10% to 25% if you are sending 11 integers or less.
Thirdly, as the inner loop comes to dominate the execution time, the difference between the algorithms decreases. Therefore, for larger amounts of data, being really clever in your program delivers increasingly diminishing returns. The 25% difference writing one int shrunk down to about 1% for 32 ints.
Finally, and this is not obvious from the wall clock chart, the improvements in performance come from a more efficient algorithm rather than from better use of the cMesh. As I improved the algorithms I could see the execution time reducing. This is more obvious in the following, somewhat surprising chart:
This chart shows the average number of clock ticks that the cores have to wait for all mesh events. If the reduction in execution time was due to a more efficient use of the cMesh then you would expect that the best performers ("Mapped" and "Random") would be waiting less than the other two strategies.
It seems that the outer loop with fewer iterations is faster at pumping out data into the mesh which is therefore more clogged. However, the increase in waiting time of the "Mapped" strategy was only 6% of the total execution time compared to 4.2% for "Pass Up" and "0 to 15". Thus the difference made a small contribution to the convergence of the strategies as the volume of data increased.
I must also add that the steady upwards trend shown in the above graph is somewhat over simplified. Initially I used 1,000 iterations. That showed the same trend but the lines jumped around all over the place. If you are measuring something that is only a small chuck of the total execution time (in this case, 4% - 6%) and something that is influenced by other factors (i.e. other core's mesh traffic) you need to repeat the test many many times.
Conclusion
Using the e_ctimer functions is a great way to test out alternative implementations. It is like using a volt meter when developing circuits. However, you may need to run your test many thousands of times to get repeatable, representative results.
The cMesh does a pretty consistent job of delivering the data. If one of the broadcast strategies was inherently better I would expect the performance difference to be maintained and even increase as the amount of data rises. If you use direct memory writes for large amounts of data, simple is probably best.
For low volumes, while some improvement is available by tweaking the delivery process, it is your program that determines the overall performance.
Up Next...
I've briefly touched on DMA transfers is a previous post. I'd like to expand this test out beyond 32 ints and compare direct memory writes with DMA transfers. This will mean getting to understand the contents of e_dma_desc_t and how that all works.
I will also include mpi_bcast if it is available in the next release of COPRTHR2. Here the big question is whether the coordination overhead imposed by MPI is more or less time consuming than using barriers to coordinate the cores.
I will also include mpi_bcast if it is available in the next release of COPRTHR2. Here the big question is whether the coordination overhead imposed by MPI is more or less time consuming than using barriers to coordinate the cores.